Contractions between Thouless transformed operators

Transforming the fundamental creation and annihilation operators to the Thouless transformed \(d\) operators raises the need to re-define the fundamental contractions of Wick’s theorem in this new basis. Since both \((d[c_n]^\mu)^\dagger\) and \((d[c_n]^\mu)\) consist only out of the fundamental bi-orthogonal operators \(^x\tilde{b}^\dagger_p\) and \(^x\tilde{b}_p\) and we know that the only non-zero contractions are

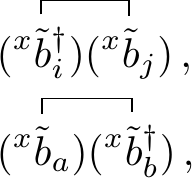
we are able to work out

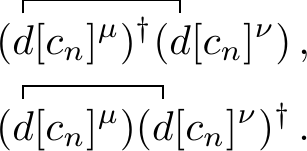
Using the full form of the \(d\) operators, the contractions can be solved by working out the contractions of all of the \(^x\tilde{b}\) operators originating from the first term, with each operator of the second term. As each of these contractions can be worked out using the fundamental contractions of these operators, the resulting expression only consists of

All other contractions vanish, as they are all of the form

Using the definitions of \({^{xw}\tilde{\mathcal{Z}}_{ai}}\) and \({^{xw}\tilde{S}_{ak}}\) results in

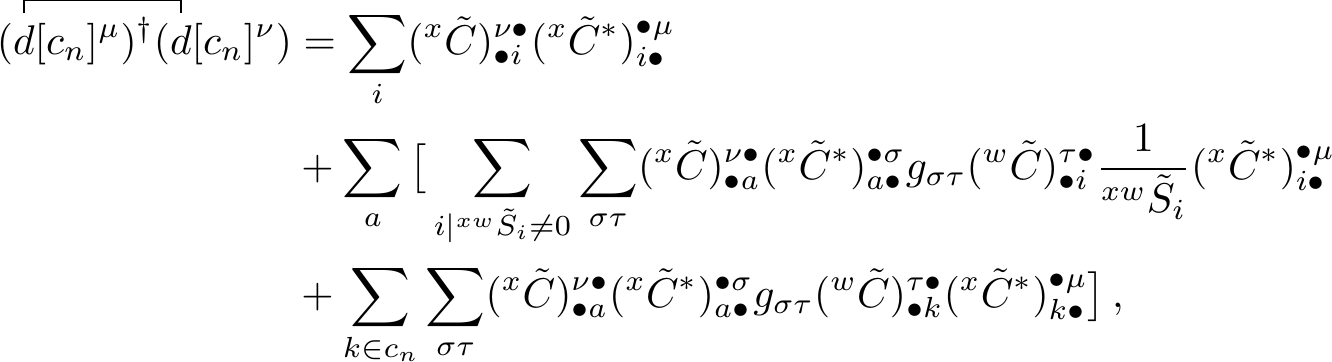
which can be simplified to

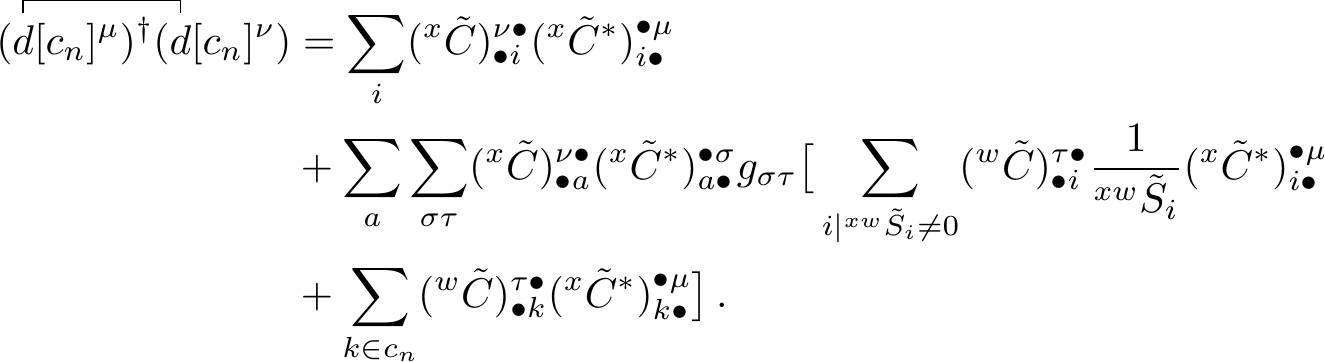
Resolving the identity in its occupied and virtual parts gives the expression \[\begin{align} \sum_p (^x\tilde{C})^{\lambda \bullet}_{\bullet p} g_{\lambda \kappa} (^x\tilde{C}^*)^{\bullet \kappa}_{p \bullet} &= 1 \\ \sum_p (^x\tilde{C})^{\lambda \bullet}_{\bullet p} (^x\tilde{C}^*)^{\bullet \kappa}_{p \bullet} &= g^{\lambda \kappa} \\ \sum_j (^x\tilde{C})^{\lambda \bullet}_{\bullet j} (^x\tilde{C}^*)^{\bullet \kappa}_{j \bullet} + \sum_a (^x\tilde{C})^{\lambda \bullet}_{\bullet a} (^x\tilde{C}^*)^{\bullet \kappa}_{a \bullet} &= g^{\lambda \kappa} \\ \sum_a (^x\tilde{C})^{\lambda \bullet}_{\bullet a} (^x\tilde{C}^*)^{\bullet \kappa}_{a \bullet} &= g^{\lambda \kappa} - \sum_j (^x\tilde{C})^{\lambda \bullet}_{\bullet j} (^x\tilde{C}^*)^{\bullet \kappa}_{j \bullet} \thinspace . \end{align}\] Substituting this expression in the contraction gives

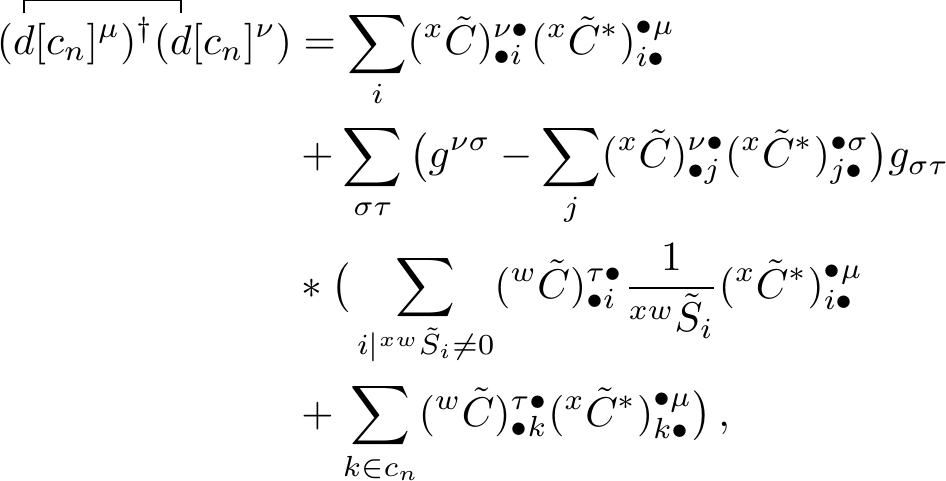
Working out the product, the co- and contravariant metrics in this equation can be cancelled out when \(\delta_{\nu \tau}=1\), results in

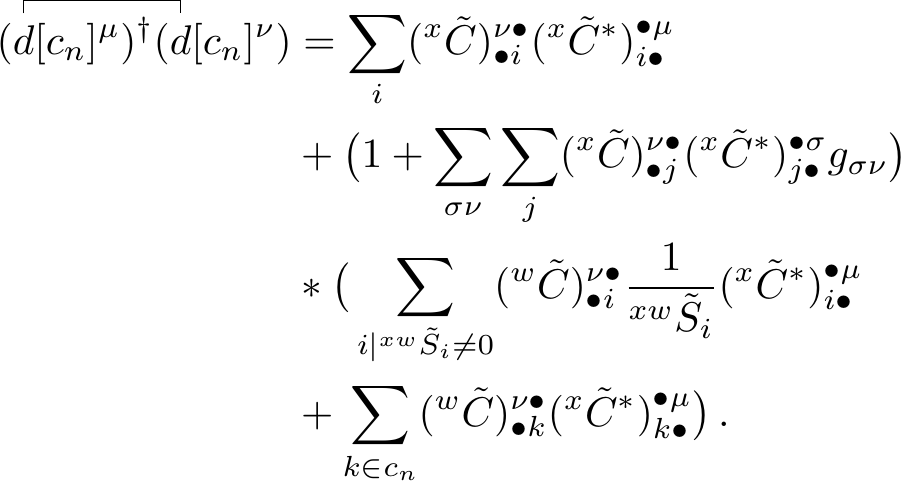
Further calculating the product yiels

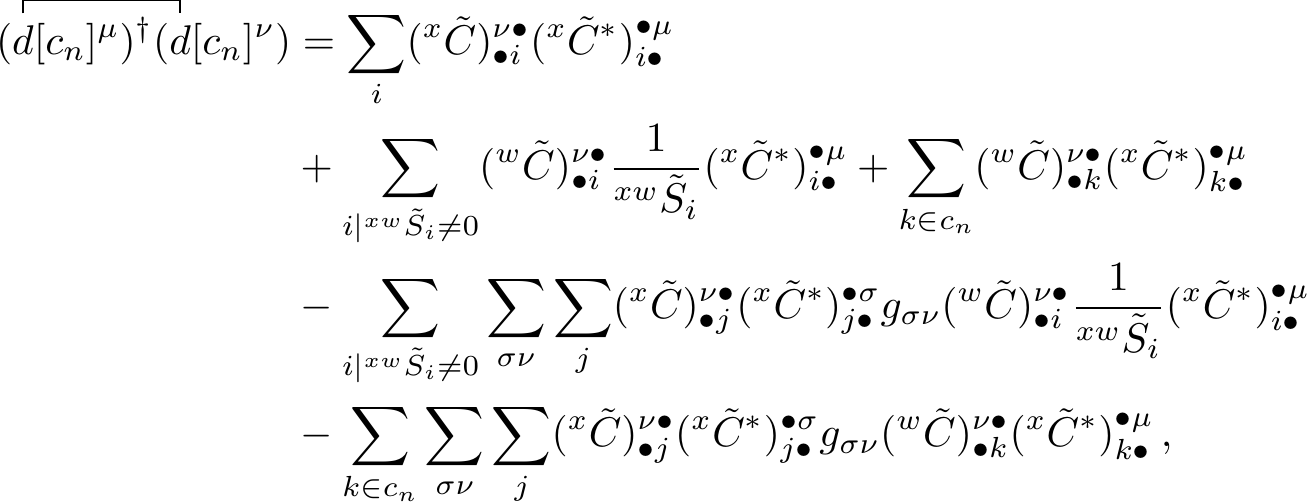
where the fourth term can be simplified becaus of the relation \[\begin{equation} \sum_{\sigma \nu} (^x\tilde{C}^*)^{\bullet \sigma}_{j \bullet} g_{\sigma \nu} (^w\tilde{C})^{\nu \bullet}_{\bullet i} = ^{xw}\tilde{S}_i \thinspace , \end{equation}\] and the final term becomes zero due to the same relation and the fact that \(^{xw}\tilde{S}_k=0\) when \(k \in c_n\). This allows us to simplify the expression to

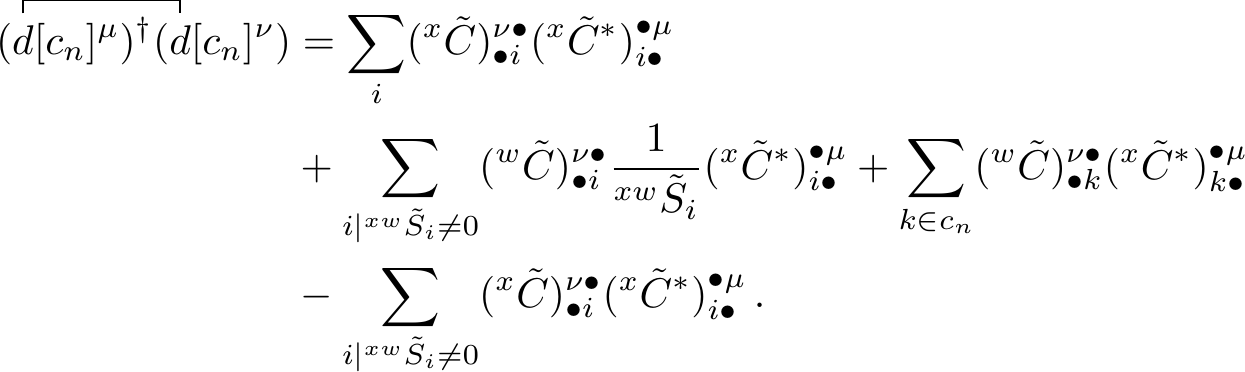
The first and last term can be combined. When doing so, the summation index will be adjusted as the summation over all \(i\) minus the summation over all non-zero overlap \(i\) equals the summation over all \(i\) where \(^{xw}\tilde{S}_i=0\). This corresponds with the index \(k\). Applying these changes in the overall expression we get

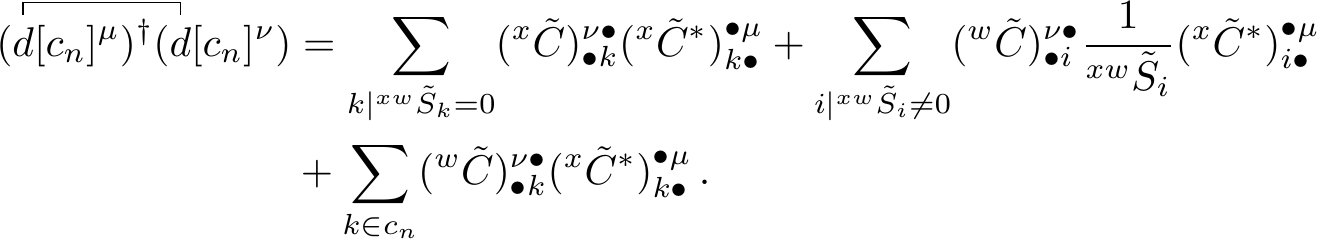
Secondly, we want to adjust the index \(k\) to be more in line with the rest. Since \(c_n\) is a compound index denoting a particular combination of \(n\) out of \(m\) zero overlap orbitals, if we change the index to loop opver all \(k\) where the orbital overlap is zero, we have to subtract the ones that are not part of the combination \(c_n\)

By introducing the definitions of the co-density, weighted co-density and co-density sum \[\begin{align} ^{xw}P^{\nu \mu}_k &= (^w\tilde{C})^{\nu \bullet}_{\bullet k} (^x\tilde{C}^*)^{\bullet \mu}_{k \bullet} \thinspace , \\ ^{xw}P^{\nu \mu} &= \sum_{k | ^{xw}\tilde{S}_k = 0} ^{xw}P^{\nu \mu}_k \thinspace , \\ ^{xw}W^{\nu \mu} &= \sum_{i | ^{xw}\tilde{S}_i \neq 0} (^w\tilde{C})^{\nu \bullet}_{\bullet i} {\frac{1}{^{xw}\tilde{S}_i}} (^x\tilde{C}^*)^{\bullet \mu}_{i \bullet} \thinspace , \\ ^{xw}M^{\nu \mu} &= {^{xx}P^{\nu \mu}} + ^{xw}P^{\nu \mu} + ^{xw}W^{\nu \mu} \thinspace , \end{align}\] the contraction becomes

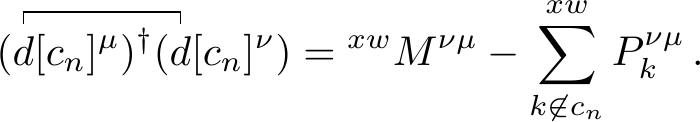
The other contraction then follows from