Generalized Slater-Condon rules

The generalised Slater-Condon rules provide a first- quantised approach for evaluating matrix elements between nonorthogonal determinants. However, they can also be recovered using the generalized non-orthogonal Wick’s theorem.

One-body operators

Consider the one-body operator \[\begin{equation} \hat{f} = \sum_{\mu \nu} f_{\mu \nu} (a^\mu)^\dagger (a^\nu) \thinspace , \end{equation}\] with matrix element

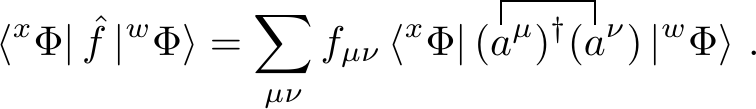
The single contraction in the asymmetric Fermi vacuum can be calculated using the derived fundamental contractions. This gives us \[\begin{equation} \bra{^x\Phi}\hat{f}\ket{^w\Phi} = \begin{cases} ^{xw}\tilde{S}\sum_{\mu \nu} f_{\mu \nu} {^{xw}M^{\nu \mu}} & \text{if $m=0$} \\ ^{xw}\tilde{S}\sum_{\mu \nu} f_{\mu \nu} {^{xw}P^{\nu \mu}} & \text{if $m=1$} \\ 0 & \text{if $m>1$} \end{cases} \thinspace . \end{equation}\] This expression can be simplified by keeping in mind that \(^{xw}M^{\nu \mu} = {^{xx}P^{\nu \mu}} + ^{xw}P^{\nu \mu} + ^{xw}W^{\nu \mu}\), where the only term that survives in case of no zero-overlap orbitals is \(^{xw}W^{\nu \mu}\) \[\begin{equation} \bra{^x\Phi}\hat{f}\ket{^w\Phi} = \begin{cases} ^{xw}\tilde{S}\sum_{\mu \nu} f_{\mu \nu} {^{xw}W^{\nu \mu}} & \text{if $m=0$} \\ ^{xw}\tilde{S}\sum_{\mu \nu} f_{\mu \nu} {^{xw}P_k^{\nu \mu}} & \text{if $m=1$ ($k$)} \\ 0 & \text{if $m>1$} \end{cases} \thinspace , \end{equation}\] where we also added the subscript \(k\) to denote that the co-density of orbital \(k\) must be taken. No summation is necessary as we know that there is only one zero overlap orbital. These are the one-body generalized Slater-Condon rules.

Two-body operators

Consider a two body operator \[\begin{equation} \hat{v} = \sum_{\mu \nu \sigma \tau} u_{\mu \nu \tau \sigma} (a^\mu)^\dagger (a^\nu)^\dagger (a^\sigma) (a^\tau) \thinspace , \end{equation}\] where \(u_{\mu \nu \tau \sigma}\) is defined as \[\begin{equation} u_{\mu \nu \tau \sigma} = \bra{\chi_\mu \xi_\nu}\hat{v}\ket{\chi_\tau \chi_\sigma} \thinspace , \end{equation}\] and the corresponding matrix element becomes \[\begin{equation} \bra{^x\Phi}\hat{v}\ket{^w\Phi} = \sum_{\mu \nu \sigma \tau} u_{\mu \nu \tau \sigma} \bra{^x\Phi}(a^\mu)^\dagger (a^\nu)^\dagger (a^\sigma) (a^\tau)\ket{^w\Phi} \thinspace . \end{equation}\] Applying Wick’s theorem results in two non-zero contractions that will survive

Both contractions can be calculated using generalized non-orthogonal Wick’s theorem, resulting in \[\begin{align} &\bra{^x\Phi}(a^\mu)^\dagger(a^\nu)^\dagger(a^\sigma)(a^\tau)\ket{^w\Phi} = \\ &\begin{cases} ^{xw}\tilde{S} \sum_{\mu \nu \sigma \tau} u_{\mu \nu \tau \sigma} \big( {^{xw}M^{\tau \mu}} \thinspace {^{xw}M^{\sigma \nu}} - {^{xw}M^{\sigma \mu}} \thinspace {^{xw}M^{\tau \nu}} \big) & \text{i $m=0$} \\ ^{xw}\tilde{S} \sum_{\mu \nu \sigma \tau} u_{\mu \nu \tau \sigma} \big( {^{xw}M^{\tau \mu}} \thinspace {^{xw}P^{\sigma \nu}} + {^{xw}P^{\tau \mu}} \thinspace {^{xw}M^{\sigma \nu}} \\ \qquad \qquad \qquad \qquad - {^{xw}M^{\sigma \mu}} \thinspace {^{xw}P^{\tau \nu}} - {^{xw}P^{\sigma \mu}} \thinspace {^{xw}M^{\tau \nu}} \big) & \text{if $m=1$} \\ ^{xw}\tilde{S} \sum_{\mu \nu \sigma \tau} u_{\mu \nu \tau \sigma} \big( {^{xw}P^{\tau \mu}} \thinspace {^{xw}P^{\sigma \nu}} - {^{xw}P^{\sigma \mu}} \thinspace {^{xw}P^{\tau \nu}} \big) & \text{if $m=2$} \\ 0 & \text{if $m>2$} \end{cases} \thinspace . \end{align}\] The case without zero overlap orbitals can be simplified analogously to the one-body operator case. The case with one zero overlap orbital can be simplified by working out the products of \(^{xw}M^{\kappa \lambda}\) and \(^{xw}P^{\eta \theta}\) and using the following relations \[\begin{align} {^{xw}P^{\kappa \lambda}} \thinspace {^{xw}P^{\eta \theta}} &= (^w\tilde{C})^{\kappa •}_{• k} (^x\tilde{C}^*)^{• \lambda}_{k •} (^w\tilde{C})^{\eta •}_{• k} (^x\tilde{C}^*)^{• \theta}_{k •} \\ &= {^{xw}P^{\kappa \theta}} \thinspace {^{xw}P^{\eta \lambda}} \\ {^{xw}W^{\kappa \lambda}} \thinspace {^{xw}P^{\eta \theta}} &= (^w\tilde{C})^{\kappa •}_{• k} \frac{1}{^{xw}\tilde{S}_i} (^x\tilde{C}^*)^{• \lambda}_{k •} (^w\tilde{C})^{\eta •}_{• k} (^x\tilde{C}^*)^{• \theta}_{k •} \\ &= (^w\tilde{C})^{\kappa •}_{• k} (^x\tilde{C}^*)^{• \lambda}_{k •} (^w\tilde{C})^{\eta •}_{• k} \frac{1}{^{xw}\tilde{S}_i} (^x\tilde{C}^*)^{• \theta}_{k •} \\ &= {^{xw}P^{\kappa \lambda}} \thinspace {^{xw}W^{\eta \theta}} \thinspace . \end{align}\] Finally we should note that in the two zero overlap orbitals case \({^{xw}P^{\tau \mu}} \thinspace {^{xw}P^{\sigma \nu}} - {^{xw}P^{\sigma \mu}} \thinspace {^{xw}P^{\tau \nu}}\) can be explicitly written as \[\begin{equation} {^{xw}P^{\tau \mu}} \thinspace {^{xw}P^{\sigma \nu}} - {^{xw}P^{\sigma \mu}} \thinspace {^{xw}P^{\tau \nu}} = \sum_{k_x \neq k_y} {^{xw}P^{\tau \mu}_{k_x}} \thinspace {^{xw}P^{\sigma \nu}_{k_y}} - {^{xw}P^{\sigma \mu}_{k_x}} \thinspace {^{xw}P^{\tau \nu}_{k_y}} \thinspace , \end{equation}\] with \(x,y \in [1,2]\). This means that there are two possible linear combinations posible: \(x=1\text{ and }y=2\) or \(x=2\text{ and }y=1\). Taking all of the above into account, the two-body generalized Slater-Condon rules become \[\begin{align} &\bra{^x\Phi}(a^\mu)^\dagger(a^\nu)^\dagger(a^\sigma)(a^\tau)\ket{^w\Phi} = \\ &\begin{cases} ^{xw}\tilde{S} \sum_{\mu \nu \sigma \tau} u_{\mu \nu \tau \sigma} \big( {^{xw}W^{\tau \mu}} \thinspace {^{xw}W^{\sigma \nu}} - {^{xw}W^{\sigma \mu}} \thinspace {^{xw}W^{\tau \nu}} \big) & \text{i $m=0$} \\ 2 {^{xw}\tilde{S}} \sum_{\mu \nu \sigma \tau} u_{\mu \nu \tau \sigma} \big( {^{xw}P^{\tau \mu}_k} \thinspace {^{xw}W^{\sigma \nu}} - {^{xw}P^{\sigma \mu}_k} \thinspace {^{xw}W^{\tau \nu}} \big) & \text{if $m=1$} \\ 2 {^{xw}\tilde{S}} \sum_{\mu \nu \sigma \tau} u_{\mu \nu \tau \sigma} \big( {^{xw}P^{\tau \mu}_{k_1}}\thinspace {^{xw}P^{\sigma \nu}_{k_2}} - {^{xw}P^{\sigma \mu}_{k_1}} \thinspace {^{xw}P^{\tau \nu}_{k_2}} \big) & \text{if $m=2$} \\ 0 & \text{if $m>2$} \end{cases} \thinspace . \end{align}\]