Gradient

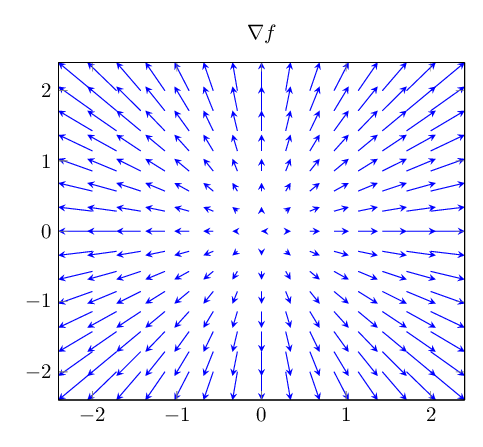
The gradient of a scalar function \(f(x, y, z)\) is denoted \(\boldsymbol{\nabla} f\) where \(\boldsymbol{\nabla}\) denotes the vector differential operator del. It is defined as the unique vector field \[\begin{equation} \require{physics} \text{grad}~f(x, y, z) = \boldsymbol{\nabla} f(x, y, z) = \qty( \pdv{f}{x}, \pdv{f}{y}, \pdv{f}{z} ) \end{equation}\] storing the all the rates of change of the function, as is illustrated in the images above. To recover the slope of \(f\) along a specific vector \(\require{physics} \vb{v}\), we can take its dot product with \(\boldsymbol{\nabla} f\): \[\begin{equation} \boldsymbol{\nabla}_{ \vb{v} } f(x, y, z) = (\boldsymbol{\nabla} f(x, y, z) ) \vdot \vb{v} \thinspace , \end{equation}\] which is nothing more than the directional derivative of a function.