Geminal pairing schemes
Literature (Karadakov, Castano, and Calais 1990b), (Karadakov, Castano, and Calais 1990a), … (overview incomplete) uses the (geminal) pairing scheme extensively.
Intuitively, a pairing scheme collects information about which pairs of orbitals (spinors or spin-orbitals) contribute to a certain geminal.
We can see that geminal pairing schemes can be represented by undirected weighted graphs, where each node represents an orbital and each edge the associated geminal coefficient, as can be seen from the figure. The corresponding geminal creator is given by: \[\begin{equation} \require{physics} \hat{\Gamma}^+ = 2 G^{21} \hat{a}^\dagger_2 \hat{a}^\dagger_1 + 2 G^{31} \hat{a}^\dagger_3 \hat{a}^\dagger_1 + 2 G^{41} \hat{a}^\dagger_4 \hat{a}^\dagger_1 + 2 G^{32} \hat{a}^\dagger_3 \hat{a}^\dagger_2 + 2 G^{42} \hat{a}^\dagger_4 \hat{a}^\dagger_2 + 2 G^{43} \hat{a}^\dagger_4 \hat{a}^\dagger_3 \thinspace . \end{equation}\]
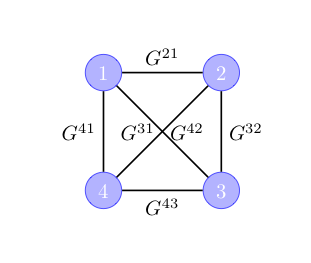
Geminal coefficients for a two-electron system described by 4 orbitals.
It is a natural question if there is a procedure to determine, given an arbitrary geminal creation operator \(\hat{\Gamma}^+_\gamma\), if a given pairing between two orbitals \(PQ\) is present in the geminal \(\gamma\). Since every separate term \(G^{PQ}_\gamma \hat{a}^\dagger_P \hat{a}^\dagger_Q\) in the most general geminal creation operator is of rank 1, we may first apply a commutator and then an anticommutator to try reduce the ultimate rank to 0. Indeed, we can calculate the nested commutator: \[\begin{equation} \comm{ \hat{a}_S }{ \comm{ \hat{a}_R }{ G^{PQ}_\gamma \hat{a}^\dagger_P \hat{a}^\dagger_Q }}_+ = (\delta_{PR} \delta_{QS} + \delta_{PS} \delta_{QR}) G^{PQ}_\gamma \thinspace . \end{equation}\]
More generally, we can ask ourselves if the geminal creation operator \(\hat{\Gamma}^+_\gamma\) contains the pairing \(PQ\) by calculating the following nested commutator: \[\begin{equation} \comm{ \hat{a}_P }{ \comm{ \hat{a}_Q }{ \hat{\Gamma}^+_\gamma }}_+ \thinspace , \end{equation}\] where the pairing strength is exactly given by the result of this nested commutator.
As an example, we can take the previous geminal creator \(\hat{\Gamma}^+\) and check that indeed a pairing of the orbitals \(1\) and \(4\) is present, since: \[\begin{equation} \comm{ \hat{a}_1 }{ \comm{ \hat{a}_4 }{ \hat{\Gamma}^+ }}_+ = 2 G^{41} \thinspace . \end{equation}\]
For a different, sparsely connected geminal pairing scheme, with corresponding geminal creation operator \[\begin{equation} \require{physics} \hat{\Gamma}^+_{\text{sparse}} = 2 G^{21} \hat{a}^\dagger_2 \hat{a}^\dagger_1 + 2 G^{32} \hat{a}^\dagger_3 \hat{a}^\dagger_2 + 2 G^{43} \hat{a}^\dagger_4 \hat{a}^\dagger_3 \thinspace , \end{equation}\] we indeed find that the pairing between orbitals \(1\) and \(2\) is present: \[\begin{equation} \comm{ \hat{a}_1 }{ \comm{ \hat{a}_2 }{ \hat{\Gamma}^+_{\text{sparse}} }}_+ = 2 G^{21} \thinspace , \end{equation}\] but the pairing between orbitals \(1\) and \(3\) is absent: \[\begin{equation} \comm{ \hat{a}_1 }{ \comm{ \hat{a}_3 }{ \hat{\Gamma}^+_{\text{sparse}} }}_+ = 0 \thinspace . \end{equation}\]
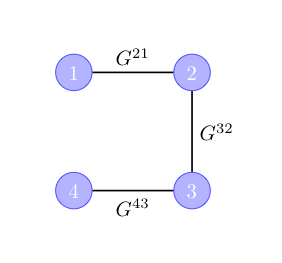
Sparse geminal coefficients for a two-electron system described by 4 orbitals.