Contractions of AO basis operators in an asymmetric Fermi vacuum

The overall matrix element in an asymmetric Fermi vacuum \[\begin{equation} \require{physics} \bra{^x\Phi}(a^\mu)^\dagger (a^\nu)^\dagger \dots (a^\sigma)(a^\tau)\ket{^w\Phi} \end{equation}\] requires the derivation of contractions between the atomic spin-orbital operators $(a^\mu)^\dagger$ and $(a^\mu)$ in this Fermi vacuum, rather than the contractions between Thouless transformed operators themselves.

Single contractions

To show how a general string of operators in an asymmetric Fermi vacuum can be evaluated using contractions, we first calculate an element of the one-body density matrix \[\begin{equation} \require{physics} {^{xw}\Gamma^{\nu \mu}_1} = \bra{^x\Phi}(a^\mu)^\dagger(a^\nu)\ket{^w\Phi} \thinspace . \end{equation}\] Assuming Wick’s theorem can be applied in some form, we expect this matrix element to be represented by the single contraction

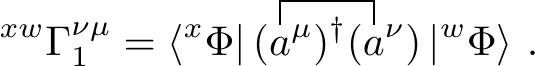
Look at the most general case, where there are $m$ zero overlap orbitals, and apply the extended thouless transformation

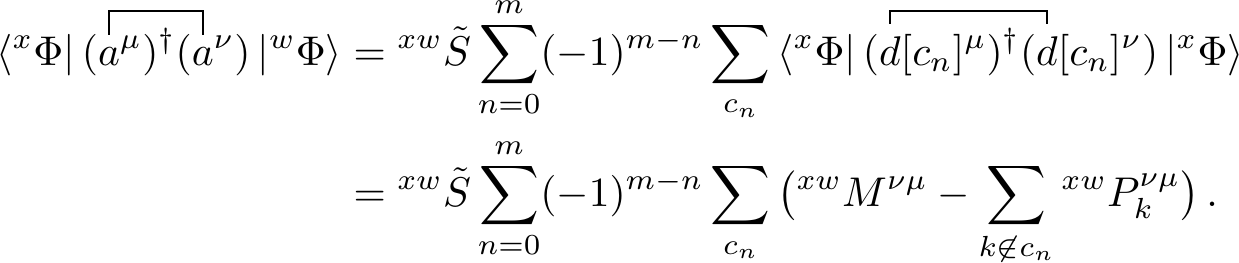
The next step requires reversing the order of summation. This rewrites any summation as \[\begin{equation} X_n = \sum^n_{i=1} i = \sum^n_{n-j=1} (n-j) \thinspace , \end{equation}\] with j ranging from $0$ to $n-1$. Applying this mathematical trick allows us to rewrite the epression as

Here, we moved ${^{xw}M^{\nu \mu}}$ outside of the summation as it does not contain $c_n$. Reversing the summation then allowed us to move the summation over $k$ out of the outer summation as well, as the modified index ranges from $0$ to $c_n - k$. This can then be written as $c_n \not \ni k$ as subtrracting $k$ from $c_n$ results in $c_n$ not containing $k$, i.e. $c_n \not \ni k$.

We now consider the terms in square brackets. Due to the definition of the extended Thouless transformation, $c_n$ defines a particular combination of $n$ out of $m$ zero overlap orbitals. The summation of $1$ over this index thus yields ${m \choose n}$. The second term is treated identically, however since this summation index is $c_n \not \ni k$, we exclude one orbital (orbital $k$) from our set, resulting in ${m-1 \choose n}$. Applying this, as well as the definition of the co-density matrix gives us

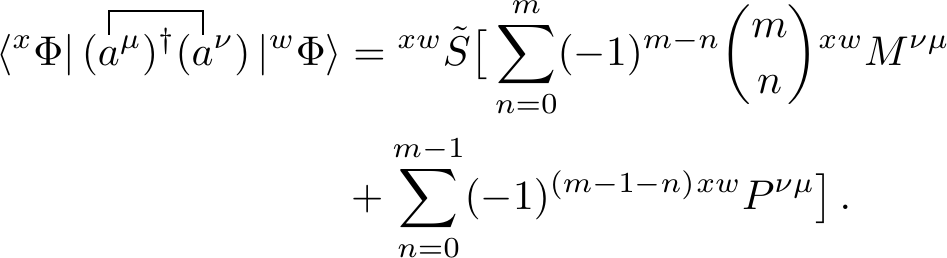
We can simplify the binomail expansions due to the relation \[\begin{equation} \sum^y_{n=0} (-1)^{y-n} {y \choose n} = \delta_{0, y} \thinspace , \end{equation}\] which results in

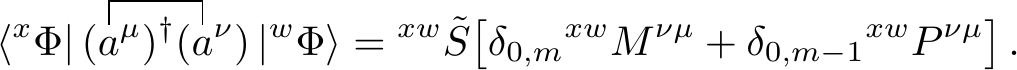
Working out the Kronecker deltas gives us

Due to the relation between the two possible contractions of the $d$-operators we also get

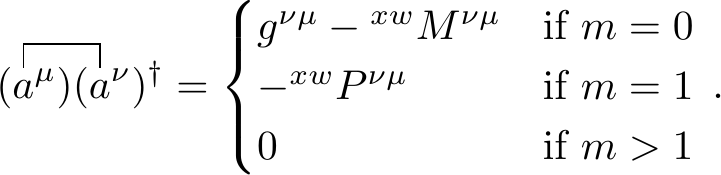
Multiple contractions

Let us now consider a two-body reduced co-density matrix element \[\begin{equation} \require{physics} {^{xw}\Gamma^{\tau \mu \sigma \nu}_2} = \bra{^x\Phi}(a^\mu)^\dagger(a^\nu)^\dagger(a^\sigma)(a^\tau)\ket{^w\Phi} \thinspace . \end{equation}\] Using Wick’s theorem we combine all possible non-zero contractions

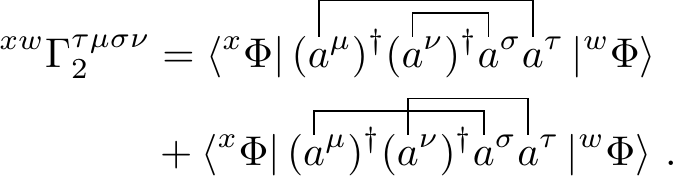
We will work out both contractions individually and add them together at the end. Let us start with the first one. The first step is to apply the extended Thouless transformation

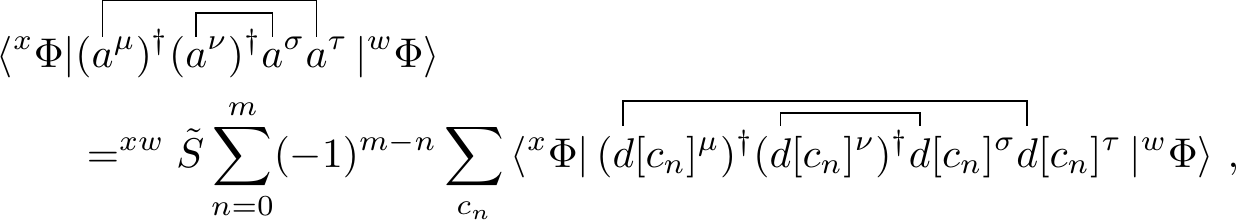
in which we can now use the contractions between the $d$-operators

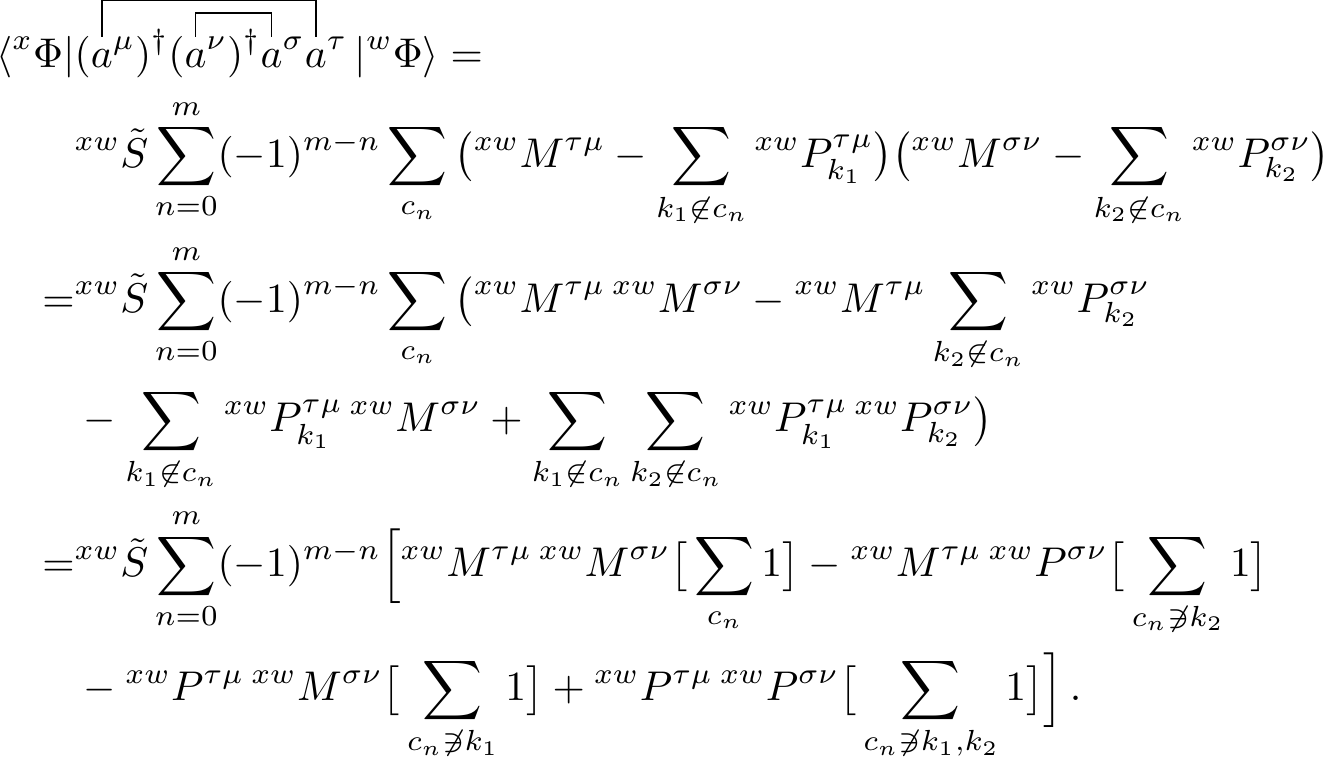
The summations in square brackets can once again be written as binomials, which in turn can be simplified to Kronecker deltas by using the relation defined earlier. This gives us

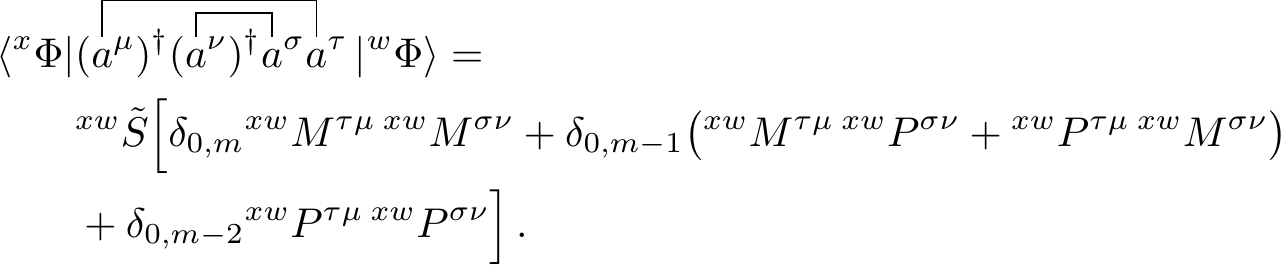
The other contraction can be analogously derived. One has to take a phase factor in account as the two contractions cross each other. This gives

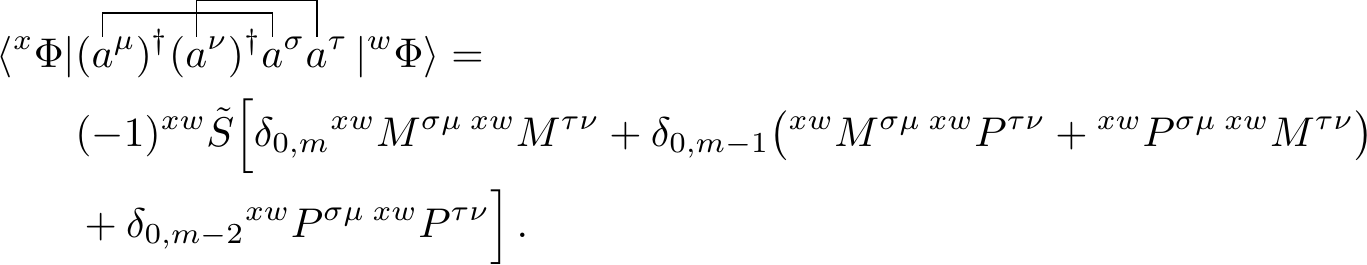
Adding the two contractions together gives us the solution for the matrix element \[\begin{align} &\bra{^x\Phi}(a^\mu)^\dagger(a^\nu)^\dagger(a^\sigma)(a^\tau)\ket{^w\Phi} = \\ &\begin{cases} ^{xw}\tilde{S} \big( {^{xw}M^{\tau \mu}} \thinspace {^{xw}M^{\sigma \nu}} - {^{xw}M^{\sigma \mu}} \thinspace {^{xw}M^{\tau \nu}} \big) & \text{i $m=0$} \\ ^{xw}\tilde{S} \big( {^{xw}M^{\tau \mu}} \thinspace {^{xw}P^{\sigma \nu}} + {^{xw}P^{\tau \mu}} \thinspace {^{xw}M^{\sigma \nu}} \\ - {^{xw}M^{\sigma \mu}} \thinspace {^{xw}P^{\tau \nu}} - {^{xw}P^{\sigma \mu}}\thinspace {^{xw}M^{\tau \nu}} \big) & \text{if $m=1$} \\ ^{xw}\tilde{S} \big( {^{xw}P^{\tau \mu}} \thinspace {^{xw}P^{\sigma \nu}} - {^{xw}P^{\sigma \mu}} \thinspace {^{xw}P^{\tau \nu}} \big) & \text{if $m=2$} \\ 0 & \text{if $m>2$} \end{cases} \end{align}\]